Minimization of DFA example using Partition Method in automata

Minimization of DFA examples using Partition Method or Equivalence Theorem:

Minimization of DFA means reduction of states.If X & Y are two states in a DFA, we can combine these two states into single state {X,Y} if they are not distinguishable i.e. equivalent or indistinguishable. Two states are said to be indistinguishable or equivalent state if δ (X, w) and δ (Y, w) are going to accepting /final states or going to non-accepting /non-final states.

Symbolically this can be represented as

1. δ (X, w) ∈ F and δ (Y, w) ∈ F

2. δ (X, w) ∉ F and δ (Y, w) ∉ F

Minimization of DFA steps/rules of minimization of DFA in automata:

Minimization of DFA questions or problems using partition method can be solved by following steps(How to do minimization of DFA):

Step1: Try to delete all the states to which we cannot reach from initial state (unreachable state)

Step2: Draw state transition table

Step3: Find out equivalent set

Step4: Draw / Construct minimized DFA

Note:

0-Equivalent Set: Try to separate non-final states from final states.

n-Equivalent Set: We take information only from previous equivalent set i.e.(n-1)-Equivalent

Set i.e. We will check, on seeing input symbol, are they going to same state or different state.

After checking if they are in same state group in previous equivalent set, then write in same group, otherwise make separate group. Follow this procedure until we get a point where we find “No change” in the state group.

Minimization of DFA Examples:

Example-1: Minimize the given DFA using partition method or construct minimized DFA using Equivalence method

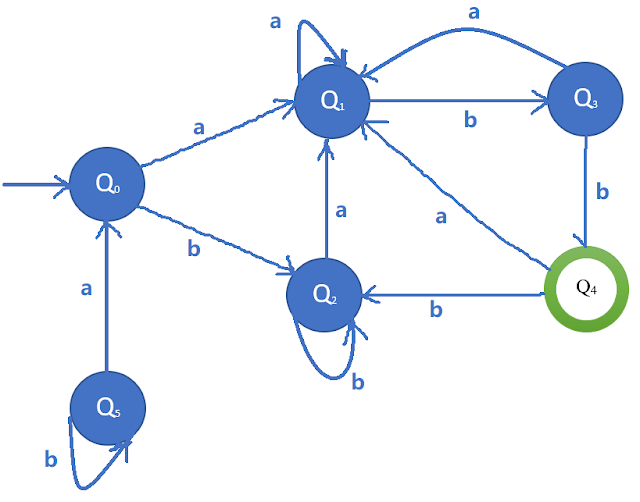Given DFA

Solution:

Step-1: Try to delete all the states to which we cannot reach from initial state

DFA Without unreachable state

Step-2: Draw state transition table of DFA:

Present State	Next State
Present State	Input a	Input b
à Q₀	Q₁	Q₂
Q₁	Q₁	Q₃
Q₂	Q₁	Q₂
Q₃	Q₁	*Q₄
*Q₄	Q₁	Q₂

Step-3: Find out equivalent sets:

0-Equivalent Set: [Q₀, Q₁, Q₂, Q₃] [Q₄]

1-Equivalent Set: [ Q₀, Q₁, Q₂] [Q₃] [Q₄]

2-Equivalent Set: [Q₀, Q₂] [Q₁] [Q₃] [Q₄]

3-Equivalent Set: [Q₀, Q₂] [Q₁] [Q₃] [Q₄]

Step-4: Draw minimized DFA:

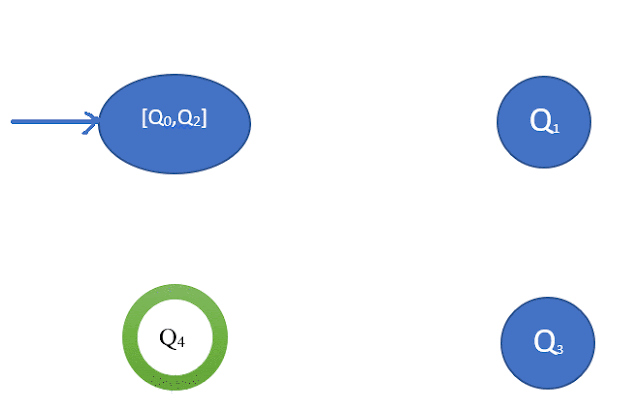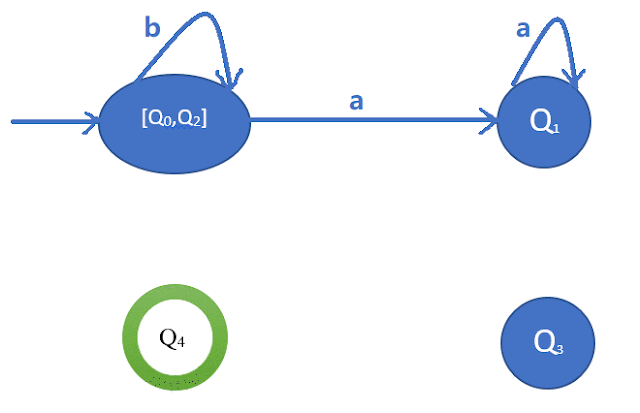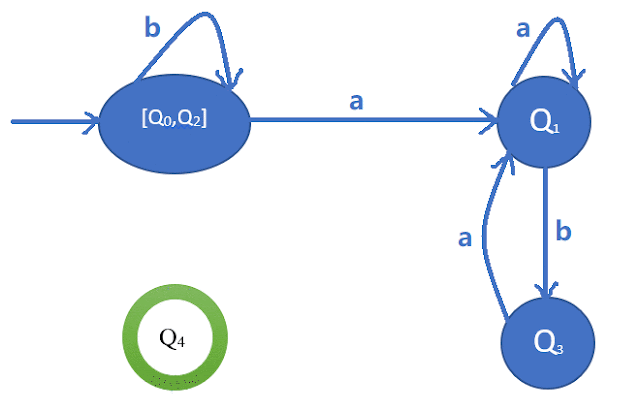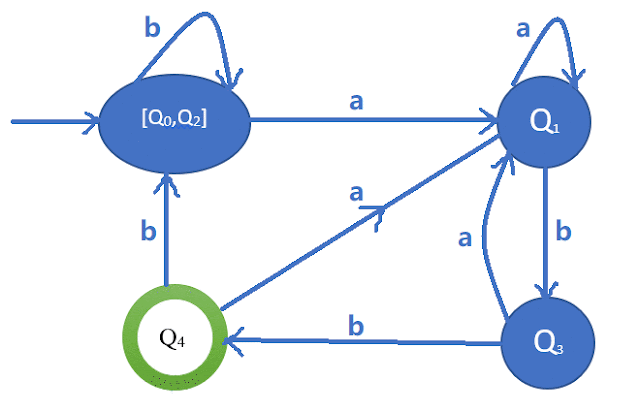Minimized DFA Diagram

Minimization of DFA Examples:

Minimization of DFA Example-1

Minimization of DFA Example-2

Minimization of DFA Example-3

Minimization of DFA Example-4

Minimization of DFA Example-5