Construct minimal DFA over ∑={a,b} which checks whether given a) Binary number is even b) Binary number is odd

SOLUTION:

∑={0,1}

a)Binary number is EVEN:

Ø  When binary number ends with 0,it is always even/When the number is divisible by 2 i.e. remainder will be 0 and the state will be represented by q₀

Ø  Since the number is even, q₀ will be final state.

Ø  So DFA can be Q={ q₀ , q₁ },∑={a,b}, q₀={ q₀},F={q₀} and δ is given by the table

1)Transition diagram:

2)Transition Table:

Present State	Next State
	Input 0	Input 1
à *q0	q0	q1
q1	q0	q1

  3)Transition function:

δ( q₀, a)= q₀     ,δ (q₀,b)= q₁

                        δ( q₁, a)= q₀     ,δ (q₁,b)= q₁

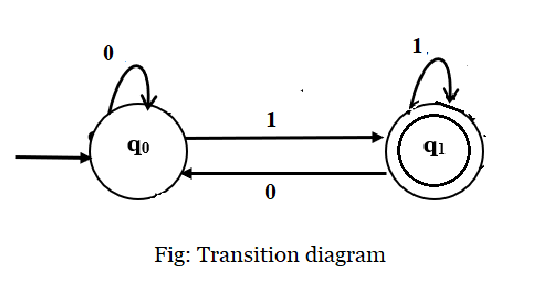
b)Binary number is ODD:

Ø  When binary number ends with 1,it is always odd / When the number is not divisible by 2 i.e. remainder will be 1 and the state will be represented by q₁

Ø  Since the number is odd, q₁ will be final state.

Ø  So DFA can be Q={ q₀ , q₁ },∑={a,b}, q₀={ q₀},F={q₁} and δ is given by the table

1)Transition diagram:

2)Transition Table:

Present State	Next State
	Input 0	Input 1
à q0	q0	q1
*q1	q0	q1

  3)Transition function:

δ( q₀, a)= q₀     ,δ (q₀,b)= q₁

            δ( q₁, a)= q₀     ,δ (q₁,b)= q₁